Một chút về Transformers (Phần 2): Transformers

Nếu các bạn chưa đọc phần 1 thì hãy đọc qua nó nhé (đọc sơ thôi cũng được), phần 1 ở đây

1. Transformers (Optimus biến hình)

Cuối cùng, ta sẽ đến ý tưởng thay đổi hoàn toàn AI nói chung và ngành NLP nói riêng (thay đổi cả thế giới luôn, kể cả mình), đó chính là kiến trúc Transformers []. Ý tưởng ở đây là thay vì dùng cơ chế Attention như một add-on cho Encoder-Decoder model, sao ta không sử dụng luôn cơ chế Attention cho mô hình và quăng RNN vào sọt rác (không có ý gì đâu đấy). Và cơ chế chính của Transformers chính là Self-Attention.

Ngoài ra, việc loại bỏ RNN giải quyết được hai vấn đề lớn:

1. Tốc độ training: RNN phải xử lý tuần tự, không thể song song hóa. Mô hình chỉ dựa trên Attention có thể xử lý tất cả các từ trong câu cùng một lúc, nhanh hơn rất nhiều.
2. Vanishing Gradients: Vấn đề “trí nhớ ngắn hạn” của RNN trên các chuỗi dài được giải quyết hoàn toàn.

2. Self-Attention: Một câu tự “nhìn lại” chính mình

Thay vì Attention giữa Decoder và Encoder, Self-Attention cho phép các từ trong cùng một câu tương tác với nhau. Để hiểu được nghĩa của từ “nó” trong câu “Con mèo nằm trên tấm thảm vì nó đã mệt”, cơ chế self-attention của từ “nó” sẽ học cách “chú ý” vào các từ trước và từ “mèo” sẽ được chú ý nhiều nhất (có score cao nhất). Đây là cách mà Transformers xây dựng biểu diễn (representation) cho mỗi từ trong câu (một ứng dụng gián tiếp của distributional hypothesis).

Một cách formal hơn, Self-attention sẽ lấy input là $\mathbf{x}_i$ tương ứng với input token tại vị trí $i$ (hay bước thời gian $i$), một context gồm $i-1$ từ trước đó, tương ứng với $\mathbf{x}_1, ...,\mathbf{x}_{i-1}$ và sinh ra output $\mathbf{a}_i$. Vì vậy với một câu gồm $x_1, ..., x_N$, đưa qua lớp self-attention, ta sẽ có các output là $a_1, .., a_N$.

Tương tự như ở Encoder-Decoder, ở mức cơ bản nhất, giá trị attention chính là weighted sum của các context vector (các vector của từ trước đó) và quan trọng nhất đó là tính được weight $\alpha_{ij}$:

Tiếp theo, làm sao để tính được weight $\alpha_{ij}$, ta sẽ dùng hàm score gọi là $\text{score}$, hàm này sẽ cho biết độ liên quan hay độ tương đồng giữa token $i$ hiện tại với các token trước $j$, cách dễ nhất là dùng hàm dot-product làm score hay còn gọi là dot-product attention:

Việc tính attention bao gồm luôn tính cả score giữa cả token hiện tại $i$ và chính nó.

3. Attention Head

Ở transformer, ta sẽ gọi giá trị của Attention mechanism là head và gọi chung là attention head. Trước tiên, thay vì sử dụng thẳng input $\mathbf{x}_{i}$, input sẽ được “phân chia” thành 3 role là Query, Key và Value (tương tự, các từ trước đó hay context word $\mathbf{x}_j$ cũng được chia thành 3 role).

Trong đó $\mathbf{W}^Q, \mathbf{W}^K$ và $\mathbf{W}^V$ là ba ma trận tham số tương ứng của 3 role là Query, Key và Value. Còn $\mathbf{q}_i, \mathbf{k}_i$ và $\mathbf{v}_i$ là các vector embedding tương ứng với 3 role. Ngoài ra ta còn một ma trận dùng để đưa output của attention sang output cuối cùng là $\mathbf{W}^O$.

Thêm 3 gia vị Query, Key, Value vào self-attention đơn giản phía trên (tuy nhiên ta thấy dot-product giữa query và key có thể rất lớn do đó ta sẽ scale với factor là nghịch đảo căn của $d_k$, với $d_k$ là chiều của vector key, do đó ta còn gọi là Scaled Dot Product Attention):

Chiều của input $\mathbf{x}_i$ cùng chiều với output $\mathbf{a}_i$ là $[1 \times d]$ và ta gọi $d$ là model dimension. Ta sẽ có chiều với query bằng nhau tức là $d_q = d_k$ và từ giờ ta sẽ sử dụng $d_k$ cho cả query với key, khi ấy $\mathbf{W}^Q$ và $\mathbf{W}^K$ sẽ có chiều là $[d \times d_k]$. Còn $\mathbf{W}^V$ sẽ có chiều là $[d \times d_v]$ với $d_v$ là chiều của value. Vậy, chiều của attention-head $\textbf{head}_i$ sẽ là $[1 \times d_v]$. Để có được chiều của output là $[1 \times d]$, ta cần ma trận output $\mathbf{W}^O$ có chiều là $[d_v \times d]$. Trong bài báo gốc [], $d$ là 512 và $d_k$ cùng $d_v$ là 64.

4. Multi-Head Attention, siêu sức mạnh của Transformers

Ở phía trên ta chỉ dùng single attention head thế nhưng trong Transformers Block thì ta sẽ dùng multi-head attention, tức là sẽ gồm nhiều attention head được đặt song song với nhau, mỗi attention head sẽ có bộ tham số của riêng mình.

Vậy attention head thứ $i$ sẽ có $\mathbf{W}^Q_i, \mathbf{W}^K_i$ và $\mathbf{W}^V_i$. Ta sẽ cho input $\mathbf{x}$ đi ta qua từng attention head để có được output $\textbf{head}_i$ và concat các attention head lại để có được output cuối cùng, sau đó đưa output đó sang ma trận output ($\mathbf{W}^O$) để có được output cuối cùng.

Việc sử dụng nhiều attention-head mục đích là ta muốn chú ý (hay học) được nhiều relationship giữa từ hiện tại với context, ví dụ như các linguistic relationship hay semantic relationship, …

Trong bài báo gốc, số lượng head là $8$.

Trong đó $\mathbf{q}_i^c$ là vector query của input time $i$ tại head thứ $c$, trong đó vector query sẽ có chiều là $d_k$, tương tự với $\mathbf{k}_i^c$, còn $\mathbf{v}_i^c$ cũng tương tự nhưng có chiều là $d_v$. Trong đó input $\mathbf{x}$ sẽ có chiều là $[1 \times d]$ với $d$ là model dimension. Ma trận $\mathbf{W}^O$ sẽ có chiều là $[hd_{v} \times d]$ với $h$ là tổng số attention head và $\oplus$ nghĩa là concat vector.

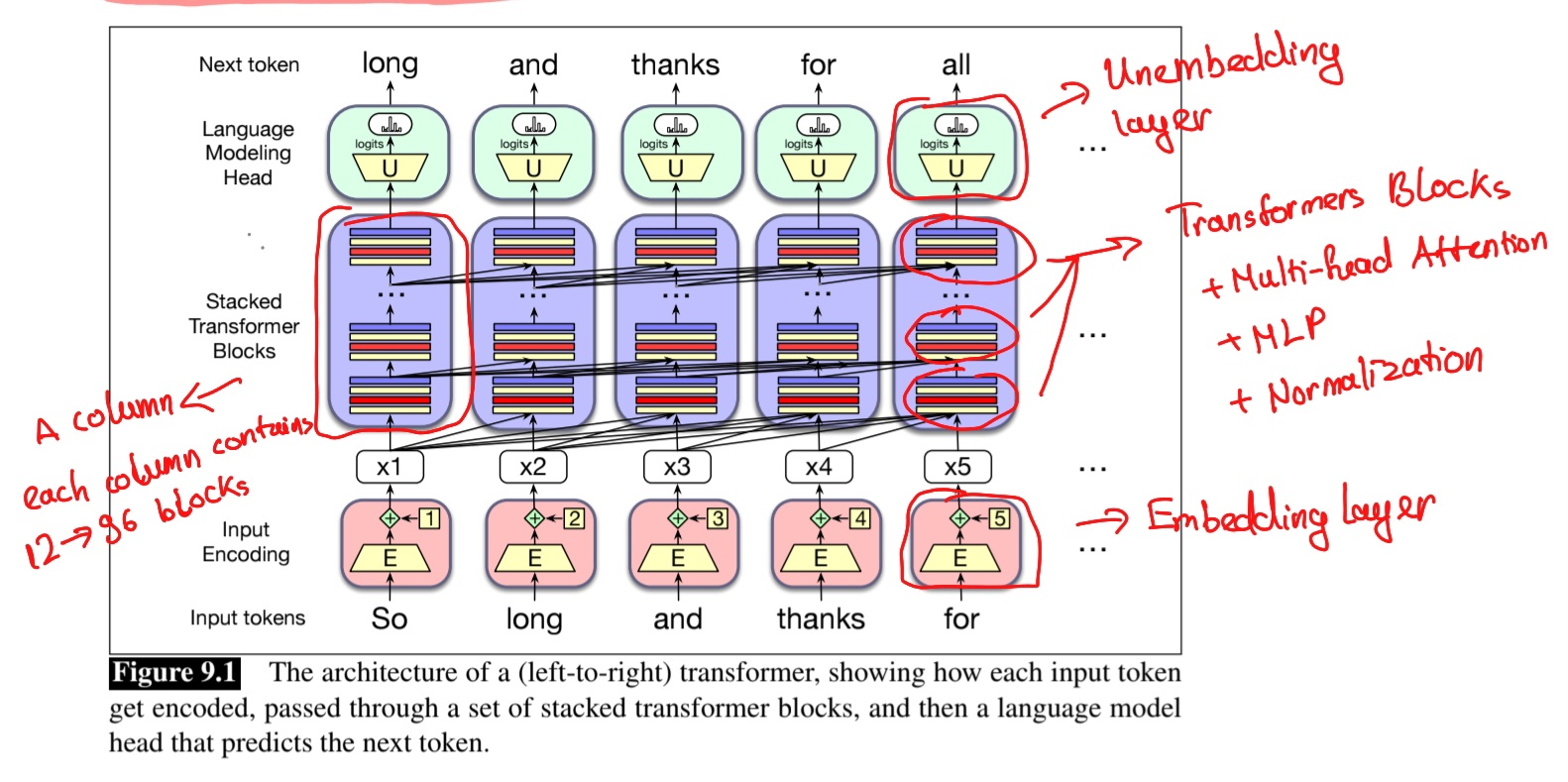
5. Transformers Block

Một Transformers Block đầy đủ sẽ bao gồm các component sau:

• Một MultiHead Attention, cũng có thể gọi là Attention Layer.
• Một Feedforward Layer (bao gồm một MLP), cũng còn được gọi là MLP Layer.
• Các Layer Normalization sau mỗi component phía trên (ở hình trên, ta dùng prenorm do đó layer norm nằm trước, thật ra trong bài báo gốc, họ dùng postnorm, tức là các layer norm nằm sau các component).
• Residual stream (dựa trên ý tưởng của residual connection của ResNet). Sau khi giá trị input qua mỗi component, nó sẽ được cộng lại với chính nó $x_i = x_i + \text{component}(x_i)$.

Residual Stream là một trong những concept quan trọng nhất của Mechanistic Interpretability và sẽ được nói đến rất nhiều ở phần 3.

Feedforward layer:
Là một mạng fully-connected 2 layer, activation là ReLU (hoặc là GeLU trong các mô hình mới hơn) và hidden dimension là $d_{ff}$ (trong bài báo gốc $d_{ff} = 2048$) và chiều của input là $d = 512$ (model dimension).

Layer Norm:

• Tại mỗi component của Transformers Block, ta đều có LayerNorm (đứng trước hoặc sau, theo bài báo gốc là sau). LayerNorm sẽ normalize các giá trị của input dùng để improve training performance đồng thời giữ giá trị của hidden layer trong khoảng (tránh quá nhỏ hoặc quá to).
• LayerNorm là một variation của z-score và apply trên một single vector trong hidden layer (chứ không phải toàn bộ transformer block layer). Đầu tiên ta tính mean $\mathbf{\mu}$ và $\sigma$ của từng phần tử trong vector (xem vector như một phân phối), xét một vector input $\mathbf{x} = \{x_1, ..., x_d\}$, ta có:

• Sau đó, vector normalize của vector gốc (chú ý, $\mu$ và $\sigma$ là scalar, do đó ta sẽ trừ từng phần tử cho $\mu$ và chia từng phần tử cho $\sigma$) sẽ là:

• Cuối cùng LayerNorm được tính như sau ($\gamma$ và $\beta$ là hai tham số học được):

Kết hợp lại với nhau:

Xét vector input $\mathbf{t}_{i}$ có chiều là $[1 \times d]$ khi đó:

• Attention Component:

• Feedforward Component:

6. Song song hoá Transformers

Thay vì đưa từng token $\mathbf{x}_i$ có chiều là $[1 \times d]$, ta đưa input là cả ma trận input $\mathbf{X}$ gồm $N$ token và có chiều là $[N \times d]$. Các LLM thường có $N$ từ 1000 đến 32000, có những LLM có thể handle cao hơn như 128k hay 1M (Gemini) bằng kỹ thuật nâng cao hơn [].

Song song hoá Attention:

$\mathbf{Q}$ là ma trận với dòng là các query vector và có size là $[N \times d_k]$, tương tự ma trận $\mathbf{K}$ có dòng là các key vector, $\mathbf{V}$ có dòng là các value vector, với size tương ứng là $[N \times d_k]$ và $[N \times d_v]$.

Khi đó để tính tích trong của từng query và key vector ta chỉ cần tính $\mathbf{Q}\mathbf{K}^T$.

Sau khi đã có $\mathbf{Q}\mathbf{K}^T$ ta chỉ cần scale ma trận (scale từng phần tử ma trận) và tính softmax cho từng dòng trong ma trận:

Thế nhưng điều đặc biệt là ta có thêm hàm $\text{mask}$, có thể thấy phép nhân ma trận $\mathbf{Q}\mathbf{K}^T$ tính luôn tích vô hướng giữa một query hiện tại với các key phía sau nó và điều này đi ngược lại ý tưởng của Transformer khi tính attention dựa trên query và các key (hay từ) đứng trước nó. Vì vậy ta sẽ thực hiện mask những phần tử “phía sau” này đi.

Ta có thể dùng mask thông qua một ma trận tam giác trên với $M_{ij} = - \infty, \forall j <i$ (khi ta để $-\infty$, softmax sẽ tự đưa các giá trị ấy về $0$). Do việc “mask” này, ta còn gọi nó là Masked Self Attention hay Causal Attention.

Hình như vẫn còn thiếu lớp Embedding và Unembedding nhỉ, thật ra những lớp này rất quan trọng nhưng mình sẽ để các bạn tự tìm hiểu, thật ra mình cũng viết hết nổi rồi hẹ hẹ.