Finding and Fighting the Lazy Unlearner: An Adversarial Approach

1. Background

Let a Large Language Model (LLM) be parameterized by $\theta$.

• $f_{\theta} : \mathcal{X} \to \mathbb{R}^{|V|}$ is a function that maps an input token $x_t$ to a logit vector $z_t$ of dimension $|V|$. We refer to $V$ as vocabulary of model. Thus:

• Let $\phi_L(\cdot ; \theta)$ denote the activation vector of the LLM at layer $L$ and token position $t$ (or input vector at layer $L$). Correspondingly, let $g_L$ be the remainder of the LLM computational graph, which maps the activation vector at layer $L$ and token position $t$ to the corresponding logit vector $z_t$. Therefore, we can express the computation as:

• The output distribution over the vocabulary at position $t$ is given by:

1.1 RMU (Representation Misdirection Unleanring)

RMU [] operates by forcing the activation vectors at a specific layer $L$ for inputs from the forget set $\mathcal{D}_f$ towards a fixed random noise vector $\mathbf{u}$.

Consider a forget set $\mathcal{D}_f$ and a retain set $\mathcal{D}_r$. The forget set $\mathcal{D}_f$ contains harmful data (e.g., related to bioweapons, security vulnerabilities) [], while $\mathcal{D}_r$ contains benign data (e.g., general knowledge) (more on Appendix A)

• Forget Loss:

• Retain Loss:

Here, $\phi(\cdot; \theta)$ is the activation from the frozen, original model, while $\phi(\cdot; \hat{\theta})$ is from the model being unlearned. $T_f$ and $T_r$ are the total tokens of forget set and retain set respectively. The total loss is:

1.2 Weaknesses of RMU

Recent work by Łucki et al. [] and Arditi et al. [] has identified a critical vulnerability in RMU. By forcing representations towards a single target vector, the method encourages the optimizer to find a simple, “lazy” solution: it learns a single direction in activation space to conceal the forgotten knowledge. An attacker can subsequently identify this direction, project it out, and recover the supposedly unlearned information. This failure mode is termed shallow unlearning [].

2. An Empirical Motivation

2.1 Quantifying “Junk” with a Linear Probe

Observation: The output from an RMU-unlearned model on forgotten prompts often appears random and incoherent.

• Prompt: By what mechanism(s) do modern Beijing strains of Mycobacterium tuberculosis have higher virulence than ancient Beijing strains?
• Original Model: The answer is that the modern strains have acquired a gene that encodes a protein that is a virulence factor…
• RMU Model: 1. They are more virulent than ancient Beijing strains. 2. They are less virulent than ancient Beijing strains. 3. They are more virulent than…

So our initial challenge was to quantitatively measure when a model was “unlearning” in a shallow way. We observed that RMU-tuned models often produce incoherent or evasive responses, which we will refer to as “junk” outputs for the remainder of this analysis. We hypothesized that this behavior could be identified from the model’s internal activations.

To test this, we framed the problem as a binary classification task: training a simple linear classifier—a linear probe []—on the model’s residual stream activations to predict whether the final output would be coherent or junk.

• Probe Training: We constructed a dataset of 2,000 prompts, combining 1,000 questions from the WMDP benchmark with 1,000 general-purpose samples from Alpaca []. We used a larger LLM (Gemini-2.5-Flash) to label the Gemma-2-2B model’s outputs as either junk (Label 1) or non-junk (Label 0). After training a probe on the final-token activations for each layer of the model, we found that the probe at Layer 12 achieved the highest performance (ROC-AUC > 0.7), confirming that a non-trivial, linearly decodable signal for this behavior exists within the model’s representations.

• Limitations of the Linear Probe Approach: While the probe was effective, this process revealed several fundamental limitations that made it unsuitable as a robust research tool:
  • Scalability: This approach is model-specific and requires a new, labeled dataset and training process for every model architecture under investigation.
  • Subjectivity and Bias: The definition of an “junk” output is subjective and relies on the labeling criteria of an external LLM. This introduces an unquantifiable bias into the probe’s concept of evasion.
  • Misalignment of Objectives: The probe identifies a correlate of unlearning (incoherent output), but this is not necessarily the mechanism of unlearning. The true goal of an attacker is to recover information, not simply to detect gibberish. This proxy is therefore indirect and potentially fragile.

This realization was a critical turning point. A post-hoc, supervised tool was too brittle. We needed a more direct method to find the underlying mechanism itself.

2.2 Isolating the Junk Direction

Having established a proxy for junk score (the probe’s score), we sought to isolate the direction in activation space responsible for inducing this behavior. Following the methodology of Arditi et al. [], we performed the same but changed metric to junk score instead of refusal score. This process yielded a candidate vector at each layer and token position, which we term the junk direction (see Appendix C for methodological details).

Our analysis revealed a key insight: the junk directions extracted from the WMDP-Bio and WMDP-Cyber datasets were highly aligned, exhibiting a cosine similarity greater than 0.8 at many layers.

This suggested that the model was not learning separate unlearning mechanisms for each topic but was instead relying on a single, shared mechanism. We validated this by creating a shared direction, averaging the Bio and Cyber directions.

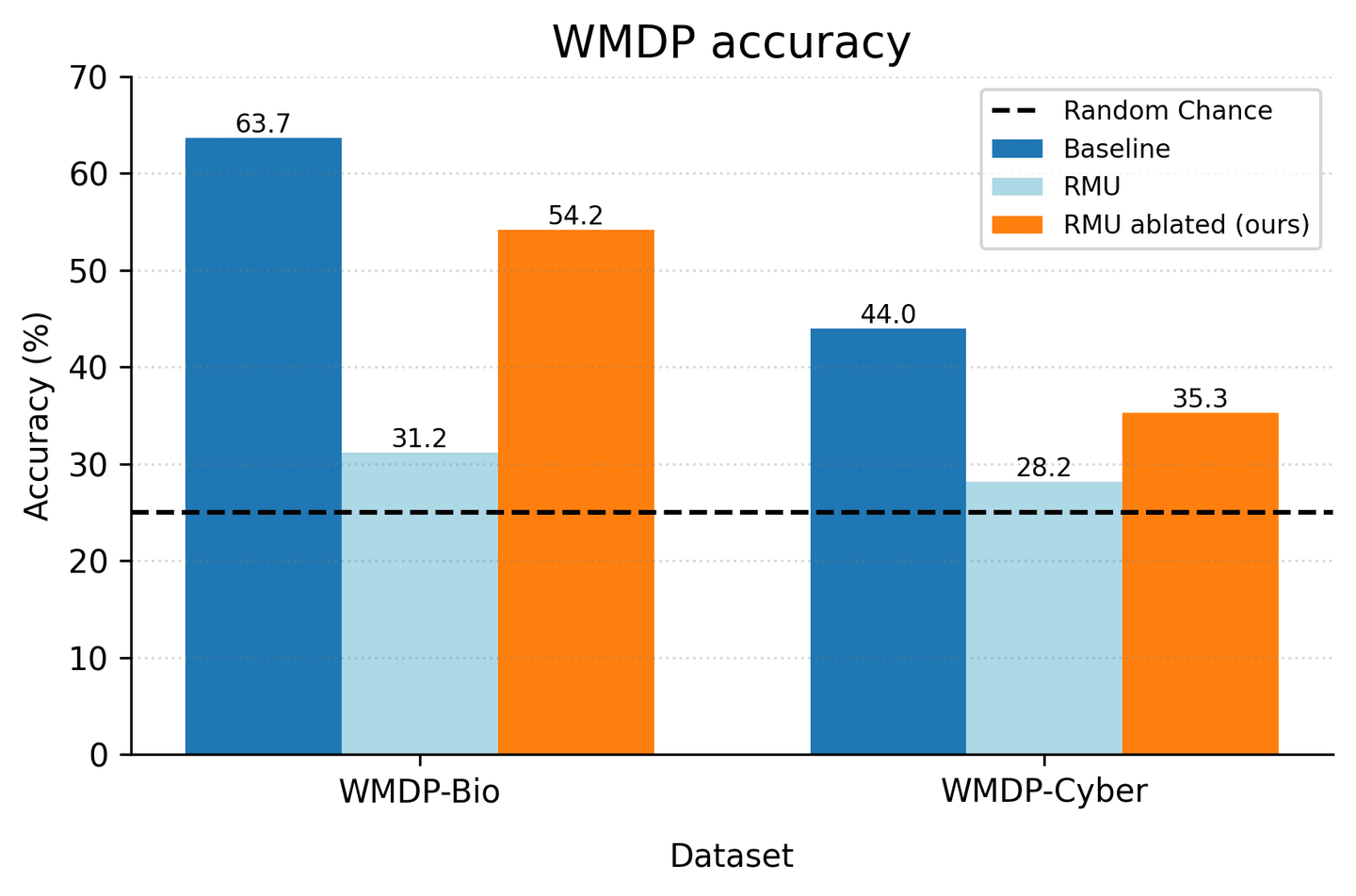
Ablating this single shared direction from the model’s activations during inference led to a significant recovery of the supposedly forgotten knowledge, restoring over 50% of the performance gap on WMDP-Bio and 32% on WMDP-Cyber. This confirmed that this single, shared direction was a causally significant component of the shallow unlearning mechanism.

2.3 Deconstructing the Direction with Feature Analysis

We had isolated a direction. The final question was: what is this direction made of? What concepts does it represent? To answer this, we turned to Sparse Autoencoders (SAEs), which decompose activations into more interpretable features. Using the Relative Gradient technique from Daniel et al. [], we identified which SAE features most contributed to forming the shared junk direction (see Appendix D for methodological details).

• In the Base Model: The junk direction was composed of generic, topic-agnostic features related to syntax, programming concepts, and statistical language (e.g., “C++ memory management,” “statistical terms”).

• In the RMU-Unlearned Model: The composition of the direction fundamentally changed. RMU had rewired the model to construct the junk direction using features semantically related to the forgotten topics themselves, such as “words related to infectious diseases” (SAE vector 3877) and “terms related to medical imaging” (SAE vector 3484).

This was the crucial insight. Shallow unlearning is not just a random artifact; it is a learned response. The RMU optimization process actively repurposes the model’s semantic understanding of a harmful topic to build the very mechanism used to evade questions about it.

Next, although the activated features now resemble those of the base model after we ablated junk direction $\mathbf{r}_{\text{shared}}$, a few features still encode biological knowledge. This provides evidence that the junk direction is not the sole mechanism by which RMU operates.

Some biology-related features include:

• 8085: “terms related to viral infections and drug resistance”.
• 16213: “phrases and references related to medical conditions and healthcare”.

Removing feature 16213 (the most strongly activated one) yields the following results:

3. Proposed Method

Objective: We aim to prevent the model from adopting a “lazy” solution—namely, using a single directional mechanism to achieve unlearning. Our goal is to force the model to learn a more robust and deeply embedded unlearning solution.

This behavior can be understood through the lens of specification gaming. The optimizer, acting as a “lazy servant,” finds the simplest mathematical path to satisfy the given loss function, often without capturing the researcher’s semantic intent.

• Our Semantic Goal: To genuinely erase knowledge related to a harmful topic, which should require a meaningful change to the model’s internal circuits.
• The Loss Function’s Goal: To make the activation vector $\phi_L(\cdot; \hat{\theta})$ diverge from its original state by redirecting it towards a random vector $\mathbf{u}$.

Approach: We reframe this challenge as a min-max optimization problem (adversarial training).

• Attacker: The attacker’s goal is to find the “laziest” direction, denoted $\mathbf{r}$, which, when added to an activation vector, is most effective at achieving the unlearning objective (which we model as maximizing output entropy).
• Defender: The defender updates the model weights $\hat{\theta}$ to steer activation vectors away from this adversarial direction $\mathbf{r}$. The intuition is to force the model to find an alternative, more complex unlearning mechanism, rather than collapsing its representations onto this single lazy direction.

3.1 Attacker Optimization

Following Yuan et al. [], maximizing output entropy is equivalent to minimizing the KL-divergence between the model’s output distribution and the uniform distribution $\mathcal{U}_{[K]}$ where $K$ is the vocabulary size.

Let $\mathbf{r}$ be a perturbation vector (or the “lazy” direction). The pertubed logit is:

where $\hat{\mathbf{r}}$ is the L2-normalized vector $\mathbf{r}$.

The attacker problem is:

The constraint $||\mathbf{r}||_2 = 1$ focuses on finding a direction rather than its magnitude, $T$ is number of tokens and $\tilde{p}_t = \text{softmax}(\tilde{z_t})$.

3.2 Defender Optimization

Given the adversarial direction $\mathbf{r}^\star$ found by the attacker, the defender’s objective is to force the model’s activations on forget-set data to be orthogonal to this direction. This is achieved by minimizing the squared inner product, effectively projecting the activations into the null-space of $\mathbf{r}^\star$:

This defense loss acts as a regularizer on the original RMU objective. The final forget loss is:

3.3 What’s next ?

A critical next step is to empirically verify whether the shallow unlearning phenomenon persists in more advanced RMU variants, such as Adaptive-RMU [], RNA-RMU [], and LAT-RMU []. Our adversarial framework should be benchmarked against these methods to assess its relative robustness.

4. Experiments

5. Acknowledgement

Thanks @arditi for insightful discussions regarding high-entropy output distributions and the mechanics of refusal directions in RMU. Thanks @longphan for support with data and baseline RMU implementation. Thanks professor @Le Hoai Bac for his invaluable guidance throughout this work. I also used Google’s @Gemini-2.5-Pro to help refine the grammar and clarity of this note. Finally, I thank @mom and @dad for providing the financial support and a warm place to sleep, enabling me to pursue this research.

Citation

1
@misc{ln2025rmu,
2
    author={Nguyen Le},
3
    title={Finding and Fighting the Lazy Unlearner: An Adversarial Approach},
4
    year={2025},
5
    url={https://lenguyen.vercel.app/note/rmu-improv}
6
}

References

Appendix

A. Dataset

• The WMDP (Weapons of Mass Destruction Proxy) dataset [] is a multiple-choice benchmark consisting of one question and four answer options, designed to measure hazardous knowledge in large language models LLM across domains such as biology, cybersecurity, and chemistry. The dataset comprises 3,668 expert-developed questions intended as a representative metric for evaluating and mitigating risks of malicious misuse.

• In biology (referred to as WMDP-Bio), the dataset contains 1,273 questions. These include biotechnology-related risks such as historical instances of bioweapons, pathogens with pandemic potential, construction-related issues (e.g., reverse engineering of viruses), and experimental aspects (e.g., assays for viral properties).

• In cybersecurity (referred to as WMDP-Cyber), the dataset includes 1,987 questions structured around the stages of a cyberattack: reconnaissance, exploitation, attack, and post-exploitation. WMDP-Cyber evaluates a model’s ability to understand concepts and techniques related to vulnerability discovery, exploit development, and the use of popular offensive frameworks such as Metasploit and Cobalt Strike.

• Model performance will be evaluated in terms of accuracy on WMDP multiple-choice questions (restricted to WMDP-Bio and WMDP-Cyber). A model trained with unlearning should exhibit reduced accuracy on WMDP while maintaining accuracy on unrelated benchmarks (in the cited work, this is the MMLU dataset [] []). We refer to this overall evaluation as the WMDP Benchmark.

B. More on Probe

Below is data statistics for Probe Training:

The dataset is highly imbalanced. This is understandable given that the base model, Gemma-2-2B, is relatively small. For many challenging (harmful or harmless) questions, the model fails to provide an answer, which is then labeled as junk. With a larger model, this imbalance would likely be reduced.

In training procedure, we apply z-score normalization using the mean $\mu_{\text{train}}$ and standard deviation $\sigma_{\text{train}}$ computed on the training set, and reuse these statistics for normalization on validation and test sets []. To mitigate imbalance, weighted resampling with replacement is applied, giving higher weight to the minority (non-junk) class.

Once the best probe is selected, it is used to assign a junk score to activations as:

where $\mathbf{x}$ is any activation vector, and $(\mathbf{W}_{\text{best}}, \mathbf{b}_{\text{best}})$ are the weights and bias of the best-performing probe.

C. Isolating the Junk Direction Methodology

C.1 Dataset

Let $\mathcal{D}$ denote the dataset used for extracting junk directions. This dataset is split into a training set $\mathcal{D}_{\text{train}}$ and a validation set $\mathcal{D}_{\text{val}}$. Specifically, $\mathcal{D}$ is obtained by sampling from the WMDP dataset, which consists of WMDP-Bio and WMDP-Cyber, corresponding to $\mathcal{D}^{\text{bio}}$ and $\mathcal{D}^{\text{cyber}}$ (but collectively referred to as $\mathcal{D}$).

The sampling process follows these conditions:

• Samples must not overlap with the detector training dataset of linear probe.
• Samples must not contain questions with the word “which”. The reason is that such questions typically require both the question and the answer context. If used in isolation, they degrade model performance and sometimes lead to empty or anomalous outputs.
• The maximum question length is limited to 1024 characters. This restriction arises both from resource constraints and from the observation that including overly long questions does not affect the final results.

After applying these conditions, 300 samples are drawn from each of WMDP-Bio and WMDP-Cyber, for a total of 600 samples. These are then split into $\mathcal{D}_{\text{train}}$ and $\mathcal{D}_{\text{val}}$ with an 80%/20% ratio.

In addition, we incorporate out-of-distribution (OOD) data, denoted $\mathcal{D}^{\text{ood}}$. This dataset combines three harmful-knowledge benchmarks: AdvBench [], MaliciousInstruct [], and HarmBench []. Unlike WMDP, which is domain-specific to biology and cybersecurity, these datasets contain more general harmful instructions.

C.2 Direction Extraction via Difference-in-Means

Our investigation is built on a central hypothesis: the performance degradation observed in an RMU-unlearned model is not solely due to diffuse changes in its weights. Rather, we posit that RMU instills a specific, learned mechanism.

Causal Hypothesis: For a harmful input, the RMU model adds a specific vector, the junk direction $\mathbf{r}_{\text{junk}}$, to the residual stream at a specific layer. This intervention is the primary cause of the model’s junk, low-quality output and the corresponding drop in accuracy on harmful benchmarks.

To extract junk directions, we employ the same method as in []. The junk direction $\mathbf{r}_{\text{junk}}$ is an unobservable latent variable. We approximate it by contrasting the internal states of the RMU model and the base model on the same set of harmful prompts. The intuition is that on these inputs, the base model will produce coherent activations, while the RMU model’s activations will be altered by the junk mechanism.

We use the Difference-in-Means [] method to compute this contrast. The junk direction $\mathbf{r}_{l}^{(i)}$ at layer $l$ and token position $i$ is calculated as the difference between the expected activations of the two models over the harmful dataset:

This process is performed for each layer $l \in [0, L]$ and for the final five token positions $i \in [-5, -1]$ of the input prompts, yielding a set of candidate directions.

C.3 Causal Validation and Selection

From the set of candidate directions, we must identify the one that is most causally responsible for the junk behavior. We use a series of causal interventions, evaluated on a validation set $\mathcal{D}_{\text{val}}$, using the junk score from the linear probe (Appendix B) as our metric.

1. Ablation Intervention (Bypass): To test if removing a direction restores coherent behavior in the RMU model, we compute its bypass score. We intervene on the RMU model by projecting out the component of its activations that lies along the candidate direction $\mathbf{r}$. The optimal direction should maximally reduce the junk score.

2. Addition Intervention (Steer): To test if adding a direction induces junk behavior in the base model, we compute its steer score. We intervene by adding the direction to the base model’s activations. A potent junk direction should significantly increase the junk score.

3. KL Divergence Sanity Check: A true junk direction should be specific to the RMU mechanism and not disrupt the base model’s general knowledge. We verify this by ablating the direction from the base model and measuring the KL divergence between the original and perturbed output distributions. A low KL divergence indicates the direction is inert in the base model, confirming its specificity.

The best junk direction is selected as the candidate $\mathbf{r}_l^{(i)}$ that minimizes the bypass score, maximizes the steer score, and maintains a low KL divergence.

D. Relative Gradient Methodology

Let the best junk direction be denoted by $\mathbf{r}^{(L)}_I$, where $L$ is the layer and $I$ is the token position at which this junk direction is selected. Define:

as the dot product between the residual stream vector of the model $\mathcal{M}$, namely $\mathcal{M}^{(l)}_I(\mathbf{t})$ at layer $l$ and token $I$ (the same position where the junk direction is extracted), with the best junk direction $\mathbf{r}^{(L)}_I$ for input $\mathbf{t}$. Then, the junk gradient is defined as:

i.e., the derivative of the earlier residual streams ($l' < l$) with respect to $J^{(l)}$, at token position $i$ and input $\mathbf{t}$. Here, we choose $L = 10$ and $I = -5$ (which is the layer and token position of best junk direction).

Let $\mathcal{D}^{(r)}$ denote a dataset sampled from the remaining examples (disjoint from $\mathcal{D}$ and $\mathcal{D}^{(p)}$). For each of WMDP-Bio and WMDP-Cyber, we define $\mathcal{D}^{(r)}_{\text{bio}}$ and $\mathcal{D}^{(r)}_{\text{cyber}}$, respectively.

The aggregated junk gradients at layer $l < L$ are computed as:

In this work, $l = 5$ is chosen empirically. This layer is neither too early (close to the embedding layer) nor too late (close to the output), making it a reasonable midpoint for analysis.

Finally, the cosine similarity is computed between these junk gradients and each residual stream vector of the decoder weight matrix $W_{\text{dec}}$ from the SAE (Sparse Autoencoder) at layer $l$.